L'atomo, le onde di materia e le nuvole di probabilità

All’inizio del XIX secolo si delinea la prima descrizione formale della teoria atomica della materia (J. Dalton 1803-1808) che è in accordo con le precedenti leggi della conservazione delle masse (A. Lavoiser,  1789) e delle proporzioni multiple (J.L. Proust, 1799). Secondo tale teoria la materia è composta da atomi, particelle microscopiche indivisibili e indistruttibili che risultano indistinguibili (hanno quindi stessa massa) per uno stesso elemento, non possono essere creati o distrutti, si combinano tra loro (anche con quelli di altri elementi) per formare i composti e sono in grado di essere eventualmente trasferiti da un composto all’altro.

Una più precisa teoria atomica permette di determinare il peso atomico degli elementi (S. Cannizzaro, 1858) che sono così riordinati – con peso atomico crescente e incolonnati per proprietà chimiche simili – evidenziando una periodicità ricorrente rappresentata in una tavola periodica (D. I. Mendeleev, 1869). E non tutte le case della tavola periodica devono essere necessariamente piene perché alcuni elementi sono ancora da scoprire.

  La discussione derivante dalla rilevazione dei raggi catodici (E. Goldstein, 1876; W. Crookes, 1880), un fascio di elettroni (J.J. Thomson, 1898), l’osservazione dei raggi canali o anodici riconosciuti come ioni positivi – atomi privati di uno o più elettroni – (E. Goldstein, 1886), nonché la successiva definizione del protone [1] decretano la nascita di quella branca della fisica conosciuta come fisica atomica.

  Elettroni e protone cancellano il concetto di indivisibilità dell’unità fondamentale della materia lasciando aperto il confronto per ipotizzarne una struttura.

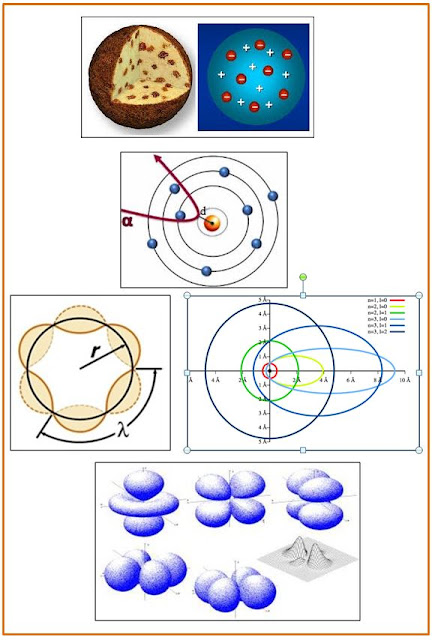
   Il primo modello atomico (J.J. Thomson, 1898), in cui le cariche negative sono distribuite e controbilanciate in una sfera omogenea positiva (una sorta di panettone con gli elettroni che rappresentano gli acini di uvetta) è sostituito, dopo l’esperimento che impiega particelle alfa come sonda, dal modello atomico planetario (E. Rutherford, 1911). In tale esperimento si utilizza, per la prima volta, un fascio di particelle proiettile provenienti dal decadimento radioattivo (di radio) inviate perpendicolarmente ad atomi bersaglio rappresentati da un sottile foglio d’oro avvolto in altro materiale ricoperto di solfuro di zinco, usato come rivelatore. È stato osservato che una particella su ottomila era riflessa ad angoli maggiori di 90°. [2]

Ipotizzando un piccolo nucleo centrale, pesante e compatto, con gli elettroni che vi gravitano attorno è possibile spiegare la diffusione osservata. Il modello atomico planetario così descritto è sì in accordo con le leggi della meccanica, ma non con quelle dell’elettrodinamica. L’elettrone, di cui è stata frattanto misurata la carica (R.A. Millikan, 1909),[3] non può girare attorno al nucleo senza irradiare energia sotto forma di onde elettromagnetiche. Proprio perché elettricamente carico l’elettrone dovrebbe, infatti, durante il suo movimento di moto non rettilineo e uniforme [4], irradiare energia; e questa sua perdita di energia dovrebbe costringerlo, seguendo un percorso a spirale, a cadere sul nucleo emettendo radiazioni a tutte le lunghezze d’onda corrispondenti alle (infinite) posizioni occupate nel suo percorso. [5]

  L’idea di applicare il quanto di energia alla struttura elettronica dell’atomo attraverso il concetto di orbite circolari quantizzate (N. Bohr, 1913), identificando stati stazionari discreti, con un preciso contenuto di energia e nei quali l’elettrone non emette radiazione elettromagnetica, indica la strada da percorrere per una possibile soluzione. Il motivo per il quale l’elettrone ruotando attorno al nucleo si presenta in uno stato stazionario è dovuto al fatto che la lunghezza della circonferenza dell’orbita 2πr risulta essere multiplo intero del valore quantizzato nh/mv ovvero mvr = nh/2πmv (dove m è la massa, v la velocità, r il raggio dell’orbita e n è un numero intero da 1 a ¥ e identifica il numero dell’orbita, il suo contenuto energetico).[6]

   L’elettrone può inoltre assorbire energia solo se questa è sufficiente a far avvenire la transazione dell’elettrone dalla prima alla seconda orbita; l’elettrone, con un salto quantico, varia il suo stato energetico da fondamentale ad eccitato ma ritornerà (dopo circa 10^-9 s) allo stato iniziale restituendo l’energia in eccesso sottoforma di radiazione elettromagnetica, in sintonia con gli spettri caratteristici di ogni elemento.

  Questo modello, che bene si adatta all’atomo di idrogeno e solo in parte ad alcuni metalli alcalini, sarà modificato introducendo orbite a diversa ellitticità  (A. Sommerfeld, 1915) aggiungendo, quindi, un secondo numero quantico, nel tentativo, parzialmente soddisfatto, di spiegare gli spettri degli altri elementi. L’originale spiegazione (H.A. Lorentz, 1900) del cosiddetto effetto Zeeman (P. Zeeman, 1896), cioè la suddivisione in triplette di una riga dello spettro della radiazione emessa da una sorgente posta in prossimità di un forte campo magnetico, è dovuta ad un terzo numero quantico che indica l’orientamento del campo magnetico creato dall’elettrone durante il suo orbitare attorno al nucleo.       

  Naturalmente è lecito chiedersi perché gli elettroni devono avere una preferenza per queste orbite, per un particolare momento angolare, legato al valore della costante di Planck.

  Nel caso delle onde elettromagnetiche tale costante ha introdotto l’aspetto corpuscolare delle onde.[7]  

  Perché non chiedersi se, questa volta, la relazione con la costante di Planck non spieghi per caso l’aspetto ondulatorio di un corpuscolo cioè dell’elettrone?[8]

  Se l’esistenza degli stati stazionari nell’atomo è spiegato utilizzando il quanto d’azione per giustificare le proprietà dell’elettrone, perché non assegnare all’elettrone un dualismo corpuscolo-onda cioè un aspetto ondulatorio?

  È dunque possibile ipotizzare che le condizioni di quantizzazione conducano all’introduzione di una componente ondulatoria degli elettroni in modo che la lunghezza d’onda di questo aspetto ondulatorio abbia un valore tale per cui l’orbita (2πr) ne contiene un numero intero, multiplo di h/mv così che possano sussistere gli stati stazionari: l’elettrone avrà un duplice aspetto, corpuscolare e ondulatorio, fondato sul quanto di azione.

  Proprio come ad ogni frequenza delle onde elettromagnetiche corrisponde un fotone con una determinata energia che ne evidenzia la caratteristica corpuscolare (p=h/λ), ad ogni particella di materia, con una determinata energia e quantità di moto, è associata un’onda caratteristica, una vibrazione, la cui lunghezza è definita dalla costante di Planck diviso la quantità di moto della particella stessa (L. De Broglie, 1924):

l = h/p

  Dato il piccolissimo valore della costante di Planck si capisce che è vano il tentativo di rilevare le onde di materia  per oggetti di massa del nostro mondo quotidiano. Una palla del peso di 1 kg che rotola ad una velocità di 1 m/s (circa 3,6 km/h, la velocità alla quale normalmente si passeggia) produce una lunghezza d’onda pari a 6,6 *10-34 m: davvero troppo piccola per essere rilevata! [9]

  Poiché le onde di materia hanno, di fatto, una lunghezza d’onda inversamente proporzionale alla quantità di moto, questa si dovrebbe manifestare, per elettroni lenti, in una regione di onde rilevabili sperimentalmente (L. de Broglie, 1924). Bombardando con elettroni dei cristalli di nichel sono state rilevate figure di interferenza sulla pellicola posta dietro al metallo, proprio come se il nichel fosse attraversato da onde, da raggi X, appunto, anziché da elettroni (C.J. Davisson, L. H. Germer; G.P. Thomson; 1927). La proprietà ondulatoria della materia si  è dunque manifestata per gli elettroni con un fenomeno legato alle onde, la diffrazione, e la materia ha davvero aspetti ondulatori!

  Le onde di materia sono associate al movimento di qualsiasi corpo ma, all’aumentare della massa e/o della velocità, diminuiscono rapidamente la loro lunghezza d’onda, tanto da far manifestare solo le proprietà corpuscolari. È proprio del tutto simile al caso diametralmente opposto in cui le onde elettromagnetiche manifestano in modo più evidente la loro seconda natura, quella corpuscolare, solo al di sopra di una certa frequenza, in virtù della quale sono capaci di espellere elettroni da un metallo dando luogo all’effetto fotoelettrico.

  Ma come possono le onde, alle quali sono associate i fenomeni di interferenza e diffrazione, manifestare proprietà tipiche dei corpuscoli? Nondimeno, come può l’elettrone, che è tipicamente un corpuscolo con massa e carica elettrica, avere proprietà ondulatorie?

  La luce manifesta aspetti corpuscolari e aspetti ondulatori o, meglio, le onde elettromagnetiche manifestano proprietà ondulatorie e corpuscolari così come le particelle hanno proprietà corpuscolari e ondulatorie: secondo il principio della complementarietà (N. Bohr, 1927), l’osservazione di uno dei due aspetti della stessa realtà fisica esclude l’osservabilità dell’altra.

  Nel mondo quotidiano le proprietà ondulatorie delle onde elettromagnetiche, quali ad esempio le onde radio, prevalgono su quelle dei corpuscoli perché l’energia dei fotoni interessati è mediamente molto piccola. E negli oggetti prevalgono le proprietà corpuscolari perché la lunghezza d’onda dell’onda associata è trascurabile se confrontata con le dimensioni dell’oggetto considerato e determina, in pratica, un continuo. Nel microcosmo, invece, a causa delle piccolissime masse in gioco, la lunghezza d’onda dell’onda di materia assume un significato importante perché ha dimensioni paragonabili a quella dell’oggetto d’indagine. [10]

  Il fatto di dover rinunciare, su scala atomica, alla netta distinzione tra onde e corpuscoli (giacché le onde manifestano proprietà corpuscolari e i corpuscoli si comportano come delle onde) evidenzia l’impossibilità di descrivere contemporaneamente questo doppio aspetto della natura definendo il limite, l’indeterminazione, dell’informazione ottenibile sperimentalmente.[11]

  La struttura elettronica dell’atomo, il concetto di orbite quantizzate, trova dunque adeguato sostegno attraverso l’idea delle onde di materia della meccanica ondulatoria. Le condizioni di quantizzazione del momento angolare non sono imposte ma derivate dalla natura ondulatoria dell’elettrone e le orbite contengono un numero intero di lunghezze d’onda pari a l = h/mv; l’elettrone può muoversi intorno al nucleo con questa lunghezza d’onda che è quella di un’onda stazionaria e, in questo modo, non irradia energia.

  Il dualismo corpuscolo-onda riesce a fornire una descrizione dell’elettrone in termini di onda [12] ma, in questo modo, non sarà possibile calcolare con precisione il raggio dell’orbita e l’impulso dell’elettrone: il modello ad orbite quantizzate è allora in contraddizione con il principio di indeterminazione.  

  Come fare dunque a descrivere l’evoluzione delle onde di materia nel tempo? L’idea del dualismo corpuscolo-onda trova la giusta dimensione matematica attraverso due vie: le equazioni di Schrödinger (E. Schrödinger, 1925) e la meccanica delle matrici (W. Heisenberg, 1925). Le due soluzioni sono equivalenti dal punto di vista fisico e descrivono la meccanica ondulatoria non relativistica.

  È stata l’equazione di Schrödinger a diffondersi più rapidamente rispetto alla meccanica delle matrici. Tale equazione, una funzione d’onda definita convenzionalmente Y (psi), descrive il propagarsi dell’onda associata al movimento di ogni particella. E se le particelle libere possono avere qualsiasi valore di energia e velocità – in quest’ultimo caso il limite massimo è rappresentato dalla velocità della luce – la situazione cambia radicalmente nel caso di particelle sulle quali agiscono delle forze. È questo il caso degli stati stazionari, quali l’elettrone nell’atomo, per i quali la funzione d’onda Y  è diversa da zero e ha quindi significato solo per determinati valori di energia. Le soluzioni delle equazioni di Schödinger definiscono perciò gli stati stabili dei sistemi fisici e la funzione Y  rende matematicamente conto alle orbite quantizzate che garantiscono la solidità atomica.

  L’atomo risulta composto da nuclei puntiformi pesanti, dove è racchiusa la carica positiva, e da elettroni, con carica negativa, che avvolgono il nucleo secondo le equazioni di Schrödinger che vincola l’onda elettronica in una particolare configurazione energetica che può essere rappresentata attraverso tre numeri quantici che identificano, rispettivamente, la distanza dal nucleo, la forma e l’orientamento spaziale delle orbite.

 Il numero quantico principale, indicato dalla lettera n, chiarisce il livello energetico dell’elettrone proporzionalmente alla sua distanza dal nucleo, può assumere solo valori interi da 1 a + ¥. Più alto è il numero più grandi sono gli orbitali e più aumenta la loro energia; spesso anziché utilizzare i numeri per i differenti strati di energia si usano le lettere K, L, M, N, O...

  Il numero quantico secondario, o angolare o azimutale, rappresentato con la lettera l, assume tutti i valori compresi in n-1 cioè 0, 1, 2, 3... Questo numero quantico, scritto frequentemente con le lettere s, p, d, f, g... specifica le caratteristiche geometriche dell’orbitale. Così, ad esempio, l’orbitale s ha la forma di una nuvola sferica (di probabilità) e l’orbitale p ha la forma di due lobi (a forma di 8) per le tre dimensioni dello spazio.

  Il numero quantico magnetico, m_l, è il numero dei differenti orientamenti che l’orbitale può assumere per effetto di un campo magnetico esterno con un valore massi mari a 2l+1, con valori compresi tra + l e -l.

  Un quarto numero quantico è necessario e specifico per l’elettrone. La suddivisione delle triplette in ulteriori righe, cioè l’effetto Zeeman anomalo, la struttura fine delle righe spettrali e gli effetti giromagnetici, si spiegano solo con la supposizione della rotazione dell'elettrone sul proprio asse (G.E. Uhlenbeck, S.A. Goudsmit, 1925). Ed è proprio questo concetto che giustifica la presenza di due elettroni nello stesso orbitale. Si può formulare il quarto numero quantico attraverso il principio di esclusione (W. Pauli, 1925): due elettroni possono occupare la stessa orbita solo se hanno il valore dello spin opposto. Il numero quantico di spin, m_s, può assumere solo due valori: +½ e -½. 

  L’interpretazione fisica della meccanica ondulatoria (M. Born, W. Heisemberg, N. Bohr, 1926) descrive il concetto di probabilità di transizione, cioè la probabilità in un dato istante che un corpo possa essere associato ad una determinata posizione nello spazio. Il quadrato della funzione d’onda Y  descrive allora il moto dei corpi in modo probabilistico. L’equazione di Schödinger è, di fatto, l’ampiezza (l’intensità, l’energia) delle onde di materia e la particella avrà più probabilità di essere localizzata nello spazio e nel tempo dove l’ampiezza della funzione d’onda Y  è grande. Allora gli orbitali degli atomi altro non sono che la funzione d’onda Y a cui sono stati assegnati i valori dei numeri quantici. E la funzione d’onda assume significato quando si considera un intorno tanto ampio da avere un’alta probabilità che l’elettrone si trovi in tale intorno. La probabilità di trovare l’elettrone in un dato punto dello spazio può essere più o meno elevata e si parla impropriamente di forma dell’orbitale.

  Frattanto, mentre l’interesse generale è rivolto alla corteccia esterna dell’atomo, si suggerisce l’esistenza di un’altra particella neutra situata nel nucleo – con una dimensione più piccola di quella dell’atomo di idrogeno – e che deriverebbe dalla combinazione di un protone ed un elettrone così da giustificare la  presenza degli isotopi (E. Rutherford, 1920).

  La scoperta del neutrone (J. Chadwick, 1932) conferma che i nuclei, che hanno una dimensione da 10.000 a 100.000 volte inferiore a quella dell’atomo, sono costituiti da protoni e neutroni in opportune combinazioni tali da spiegare le tavole dei pesi e dei numeri atomici.

  Elettrone, protone e neutrone – tre sole particelle – e un’unica forza, quella elettromagnetica, per spiegare le molteplici proprietà della materia (la forza gravitazionale è considerata solo nel macrocosmo).

  Ma se il microcosmo è costruito con tre particelle e governato da un’unica forza, che agisce grazie al fotone, il problema della compattezza del nucleo non è comunque risolto: come possono stare uniti assieme protoni e neutroni? I protoni si dovrebbero addirittura respingere tra loro e sui neutroni, privi di carica elettrica,  la forza elettromagnetica non può agire! È fin troppo evidente la criticità della stabilità nucleare…

   A complicare ulteriormente questa visione c’è anche la problematica relativa al decadimento b. Lo studio dei raggi b nel decadimento radioattivo ha già dimostrato che esso può avvenire secondo un’ampia gamma di energie (J. Chadwick, 1913). L’energia di tali raggi sommata a quella del nuovo nucleo prodotto (con numero atomico immediatamente superiore a quello originario) non coincide però con l’energia dell’atomo radioattivo prima del decadimento (J. Chadwick, C.D. Ellis, W. A. Wooster, 1929). All’aumentare o al diminuire dell’energia dell’elettrone emesso nei raggi b non corrisponde, come invece ci si aspetta, una minor o maggior energia del nuovo nucleo prodotto. Come spiegare questa mancanza di energia?

---

[1] Lo studio sugli ioni positivi porta a suggerire il nome di protone, dal greco pròton primo (componente del nucleo) per la particella identificata come il nucleo dell’atomo di idrogeno (E. Rutherford, 1919-1920).

[2] Il solfuro di zinco emette scintille luminose quando viene colpito da particelle alfa; è consuetudine ricordare lo stupore dello stesso Rutherford attraverso le sue parole “(…) è come sparare un proiettile da 15 pollici su un foglio di carta velina e vederlo tornare indietro a colpirti (…).”

[3] Molto vicino al valore attuale, 1,6*10-19 Coulomb oppure 4,8*10-10 ues (unità elettrostatiche).

[4] Soggetto cioè ad accelerazione radiale.

[5] Tutto questo forse sottovalutando la spiegazione di come possono restare unite in un nucleo compatto particelle con la stessa carica elettrica senza subire l’effetto di repulsione l’una con l’altra.

[6] Conseguentemente r = n(h/2π)/vm.

[7] L’effetto fotoelettrico assegna alla propagazione delle onde elettromagnetiche un comportamento discontinuo, di tipo corpuscolare e l’effetto Compton ne ha conferma la validità.

[8] Più in generale, questo strano dualismo di onde e corpuscoli deve forse essere sempre considerato ogni volta che ci ritroviamo la costante di Planck?

[9] Anche riducendo di 1.000.000 di volte la massa la lunghezza d’onda, pari a 6,6 *10^-28, non può essere rilevata.

[10] Sebbene i valori trascurabili nella fisica classica assumono prepotentemente significato nel microcosmo, il principio di corrispondenza dimostra che è sempre la meccanica classica il limite a cui tende la meccanica quantistica quando si assegnano valori molto grandi ai numeri quantici.

[11] V. post il principio di indeterminazione.

[12] Come un pacchetto di onde.